Detecting Clicks on Rotated Rectangles
Normally in web application development, clicks are a matter of listeners. Either a click hit a thing or it didn’t. When using the HTML5 canvas, this isn’t the case. Images and features are rendered onto it, but you can’t attach a listener to them. Instead, you monitor where these elements visually reside versus where clicks land.
If an object is rectangular and will never rotate, the solution is easy. If click X is between object start X and object end X, and click Y likewise, then it hit. If not, it didn’t.
In this post we’ll construct a simple series of functions for determining the same thing if the rectangle has rotated, then look at how the idea can apply to more complex shapes. Nothing new or groundbreaking, and nothing language-specific — consider this a StackOverflow answer.
Visualization
For a developer who hasn’t mathed in a while, this can seem tricky at first. Once you see a few images it’s perfectly sensible.
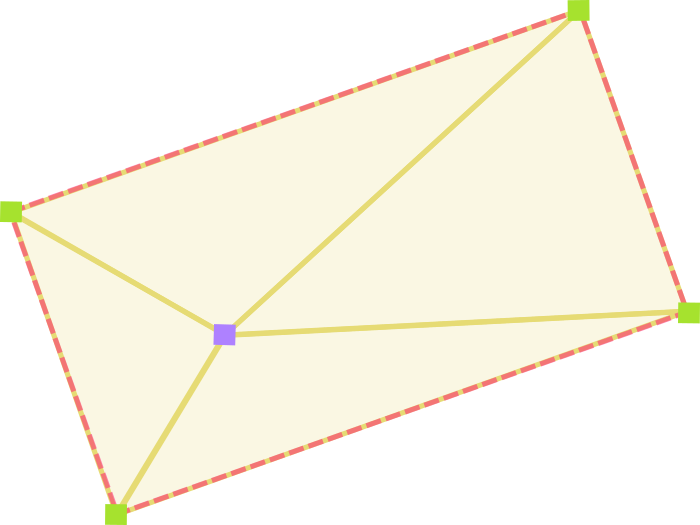
We’ll be drawing four triangles. Each one consists of the click point and two vertices of the object. We then compare the area of the object to the combined area of the triangles. If they’re the same, the click had to be in the object. If the triangles are larger, the click couldn’t have been in the object.
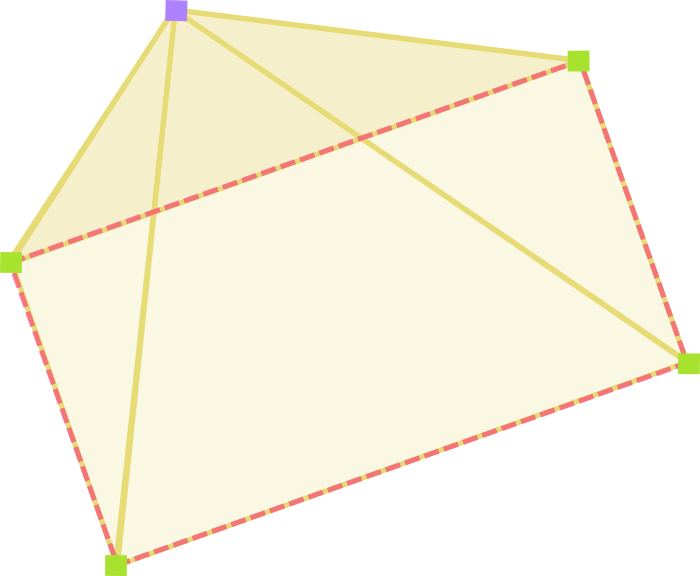
How much it’s rotated doesn’t matter. Where it’s at doesn’t matter. That’s literally all there is to this.
First things first
To figure out if the click hit, we’ll need four pieces of data:
- The coordinates of the click
- The position of the rectangle
- The size of the rectangle
- The angle of rotation of the rectangle
Those last three pieces we’re just putting together so we can find the vertices. Once we know the click position and the vertex positions, figuring out if the click hit is easy.
Finding the vertices
Since you’re probably not tracking the individual locations of the vertices and are instead tracking the position of the object, you’ll want to start with a function that can find these by the object’s size and position. How this will be done is hugely variable depending on where you’re measuring from (tracking left top? center?) and if/how the object has been scaled.
If we pretend like there’s no scaling or rotation and we’re measuring from left and top, the function may initially look like this:
// Find vertices before taking rotation into account
function findRectVertices(position, size) {
var left = position[0];
var right = position[0] + size[0];
var top = position[1];
var bottom = position[1] + size[1];
return {
LT: [ left, top ],
RT: [ right, top ],
RB: [ right, bottom ],
LB: [ left, bottom ]
};
}Since this doesn’t take into account rotation yet, we’ll need a utility function to find a point’s new location after it’s been rotated by X degrees around another point:
/**
* Find point after rotation around another point by X degrees
*
* @param {Array} point The point to be rotated [X,Y]
* @param {Array} rotationCenterPoint The point that should be rotated around [X,Y]
* @param {Number} degrees The degrees to rotate the point
* @return {Array} Returns point after rotation [X,Y]
*/
function rotatePoint(point, rotationCenterPoint, degrees) {
// Using radians for this formula
var radians = degrees * Math.PI / 180;
// Translate the plane on which rotation is occurring.
// We want to rotate around 0,0. We'll add these back later.
point[0] -= rotationCenterPoint[0];
point[1] -= rotationCenterPoint[1];
// Perform the rotation
var newPoint = [];
newPoint[0] = point[0] * Math.cos(radians) - point[1] * Math.sin(radians);
newPoint[1] = point[0] * Math.sin(radians) + point[1] * Math.cos(radians);
// Translate the plane back to where it was.
newPoint[0] += rotationCenterPoint[0];
newPoint[1] += rotationCenterPoint[1];
return newPoint;
}Modifying our previous findRectVertices function to also use rotation may then look like this, assuming we’re rotating objects around their center:
/**
* Find the vertices of a rotating rectangle
*
* @param {Array} position From left, top [X,Y]
* @param {Array} size Lengths [X,Y]
* @param {Number} degrees Degrees rotated around center
* @return {Object} Arrays LT, RT, RB, LB [X,Y]
*/
function findRectVertices(position, size, degrees) {
var left = position[0];
var right = position[0] + size[0];
var top = position[1];
var bottom = position[1] + size[1];
var center = [ right - left, bottom - top ];
var LT = [ left, top ];
var RT = [ right, top ];
var RB = [ right, bottom ];
var LB = [ left, bottom ];
return {
LT: rotatePoint(LT, center, degrees),
RT: rotatePoint(RT, center, degrees),
RB: rotatePoint(RB, center, degrees),
LB: rotatePoint(LB, center, degrees)
};
}Calculating the areas
Now that we have all the necessary points, all that’s left are three things:
- Calculate the area of the rectangle
- Calculate the area of the triangles
- Compare the two
If you recall high school geometry, point two is the loaded one there. To find the area of an unknown triangle we’d use Heron’s formula, but first the distances of each side will be needed. The two utility functions may look like this:
/**
* Distance formula
*
* @param {Array} p1 First point [X,Y]
* @param {Array} p2 Second point [X,Y]
* @return {Number} Returns distance between points
*/
function distance(p1, p2) {
return Math.sqrt( Math.pow(p1[0] - p2[0], 2) + Math.pow(p1[1] - p2[1], 2) );
}
/**
* Heron's formula (triangle area)
*
* @param {Number} d1 Distance, side 1
* @param {Number} d2 Distance, side 2
* @param {Number} d3 Distance, side 3
* @return {Number} Returns area of triangle
*/
function triangleArea(d1, d2, d3) {
// See https://en.wikipedia.org/wiki/Heron's_formula
var s = (d1 + d2 + d3) / 2;
return Math.sqrt(s * (s - d1) * (s - d2) * (s - d3));
}With those functions ready, we can now write a complete function that performs the three bullet points and returns a simple True or False:
/**
* Determine if a click hit a rotated rectangle
*
* @param {Array} click Click position [X,Y]
* @param {Array} position Rect from left, top [X,Y]
* @param {Array} size Rect size as lengths [X,Y]
* @param {Number} degrees Degrees rotated around center
* @return {Boolean} Returns true if hit, false if miss
*/
function clickHit(click, position, size, degrees) {
// Find the area of the rectangle
// Round to avoid small JS math differences
var rectArea = Math.round(size[0] * size[1]);
// Find the vertices
var vertices = findRectVertices(position, size, degrees);
// Create an array of the areas of the four triangles
var triArea = [
// Click, LT, RT
triangleArea(
distance(click, vertices.LT),
distance(vertices.LT, vertices.RT),
distance(vertices.RT, click)
),
// Click, RT, RB
triangleArea(
distance(click, vertices.RT),
distance(vertices.RT, vertices.RB),
distance(vertices.RB, click)
),
// Click, RB, LB
triangleArea(
distance(click, vertices.RB),
distance(vertices.RB, vertices.LB),
distance(vertices.LB, click)
),
// Click, LB, LT
triangleArea(
distance(click, vertices.LB),
distance(vertices.LB, vertices.LT),
distance(vertices.LT, click)
)
];
// Reduce this array with a sum function
// Round to avoid small JS math differences
triArea = Math.round(triArea.reduce(function(a,b) { return a + b; }, 0));
// Finally do that simple thing we visualized earlier
if (triArea > rectArea) {
return true;
}
return false;
}Common issues
By far the most frequent annoyance with this approach when working in the DOM is going to be getting good position numbers. So many variables can throw a wrench in how you’re measuring where the object is. If your reported object position doesn’t match up with the reported mouse or touch position, all of the above is useless.
Look for situations in which clicking near something instead of on it reports a hit, then try to identify elements that match the size of the inaccuracy. Everything from margins on the HTML or body elements, borders on divs, document scroll position, and box-sizing settings can play havoc on your ability to get clean measurements that match up with what’s plainly visible.
Going farther
This method isn’t just good for rectangles. It would be straightforward to apply to triangles, too, or for any other convex polygon. Consider how you might implement the ability to check if a click landed inside a hexagon. As a brain teaser, what would happen on a concave polygon?